Escalas logarítmicas

Por vezes, é necessário apresentar dados graficamente. É uma forma excelente de se apresentar informação de forma eficiente e até apelativa. No entanto, um dos aspetos a ter em conta é a escala do gráfico em questão: para além de ver se começa em 0, como mencionado no post Escalas que não começam em 0 (link no fim do texto), é importante ver se é linear, ou seja, se é a que esperamos ver com mais frequência – a diferença entre valores consecutivos no eixo vertical é a mesma para todas as secções do eixo. Ou seja:

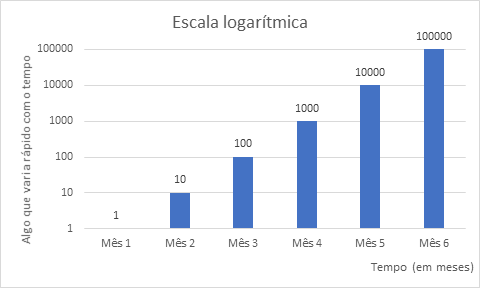
Em ambos os gráficos, temos exatamente os mesmos dados: algo num mês tinha valor 1, no mês seguinte 10, no seguinte 100, etc, como se vê nos valores acima de cada barra. Mas porque é que a variação entre meses parece muito diferente entre os dois gráficos? Não são os mesmos dados? A resposta está na escala vertical: no primeiro gráfico vemos que se “salta” do 0 para 20000, de 20000 para 40000, de 40000 para 60000, etc. Ou seja, cada “salto” é de 20000.

Mas, no segundo gráfico, passa-se de 1 para 10, e de 10 para 100… Ou seja, o 1º “salto” na escala vertical é de 9 unidades (10 menos 1), mas no 2º é de 90 (100 menos 10), e por aí em diante. Assim, a diferença entre se passar de 10 para 100 entre os 2º e 3º meses, aparenta ser a mesma que passar de 100 para 1000 no 4º mês, apesar da diferença ser 10 vezes maior. A uma escala num gráfico com este comportamento chama-se escala logarítmica.

Mas, então, porque quê usar a tão estranha “escala logarítmica”? Não seria mais fácil usar a linear sempre?

Note-se que para grandezas que variam muito rapidamente, é mais cómodo usar a segunda escala. No primeiro gráfico os valores mais baixos são praticamente indistinguíveis, enquanto que na segundo não.

---

Exemplo concreto:

É mais fácil explicar este conceito através dum exemplo concreto. Abaixo temos um gráfico que indica, para 40 dias, o número de casos confirmados de Covid-19 por dia, começando no dia em que foi confirmado o centésimo caso em cada país.

À primeira vista, podemos achar que a Espanha e a Itália , por volta do 30º dia, têm quase a mesma diferença entre número de casos entre si que a Nova Zelândia e a Austrália por volta do 12º dia. Mas estaríamos errados: a Nova Zelândia, no último dia para o qual estão apresentados dados, tinha cerca de 1000. E a Austrália estava num valor aproximadamente a meio entre os 1000 e os 10000: ou seja, 5500. Assim, a diferença entre os dois países seria de cerca de 4500 casos, neste dia.

Já entre a Espanha e a Itália é bastante diferente: No 30º dia, a Espanha tinha cerca de 100000 casos. A Itália tinha cerca de 1/10 da diferença entre 100000 e 10000 a menos: ou seja, cerca de 9000 casos a menos, 92000. Assim, na parte mais acima do eixo do nº de casos, ou seja, do eixo vertical, a variação é muito mais brusca que na parte de baixo. Ou seja, 1cm neste eixo vertical não corresponde sempre à mesma diferença. Uma curva que parece estar a estagnar na parte superior do gráfico, pode, na verdade, ser na mesma uma variação mais brusca que uma curva que pareça mais abrupta na parte inferior. Ou seja, analisar este gráfico dizendo “Por volta do entre o 20º e o 25º dia, na Austrália, houve um aumento do número de casos equivalente ao da Espanha entre o 30º e o 35º dia” está errado.

Quando na escala dum gráfico a “distância” no papel, ou no ecrã, entre 100 e 1000 (900 números de diferença) é a mesma que entre 1000 e 10000 (9000 números de diferença): é preciso saber, que este gráfico requer que se olhe com mais atenção!

Fonte do exemplo:

JHU CSSE

---

Mais sobre logaritmos:

Esta é a forma intuitiva para entender que não deve interpretar este gráfico da mesma forma que um gráfico “normal”. Estas escalas são muito úteis para cientistas apresentarem dados cujos valores variam muito significativamente.

Mas para se entender que, ao invés de confusas, são uma ferramenta muito natural para apresentar determinados dados, analisemos casos em que podemos encontrar comportamentos logarítmicos. Por exemplo, a famosa escala de Richter, que indica a severidade de um sismo, é logarítmica, de base 10. O que isto significa é que um sismo com magnitude, por exemplo, 5 na escala de Richter tem uma amplitude 10 vezes superior a um à qual seja atribuído 4; e 10x10=100 superior a um com magnitude 3, 10x10x10=1000 vezes superior a um com magnitude 2, etc. Ou seja, subir de 1 para 2 na escala de Ritcher não significa que o sismo ficou duas vezes mais intenso: significa que ficou dez vezes mais intenso.

Outro exemplo de unidade logarítmica é o decibel, que se usa para medir a intensidade de correntes e voltagens elétricas, entre outras grandezas, relativamente a valores de referência. Também é comumente utilizada para comparar intensidades sonoras, uma vez que o ouvido humano responde de modo logarítmico à potência acústica. Até a unidade que mede o brilho das estrelas, a magnitude aparente, é logarítmica: o olho humano também responde desta forma à intensidade luminosa.

Vemos, assim, que usar escalas logarítmicas, quando adequado, é espelhar o comportamento da natureza, e é muito útil desde que quem transmite e quem consome a informação entenda como elas funcionam.

---

Dê a sua opinião!

Conteúdo relacionado:

Escalas que não começam em 0